查看更多
密码过期或已经不安全,请修改密码
修改密码
壹生身份认证协议书
同意
拒绝

同意
拒绝

同意
不同意并跳过





作者:诸暨市中心医院 冯璐霏

整篇文章思维导图:
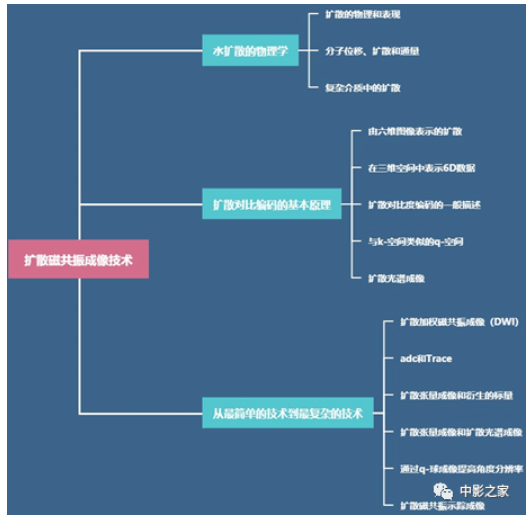
第一部分:水的扩散物理学
扩散的物理和表现
分子扩散,或布朗运动,最先由爱因斯坦在1905年正式提出。术语分子扩散指的是流体中的任何类型的分子(如水)在被热能搅动时位置被随机置换的概念(图1)。在一杯水中,分子的运动完全是随机的,只受容器边界的限制。从统计来看,可以用位移分布来描述这种随机的运动。位移分布就是分子在特定方向和特定距离上发生位移的概率。
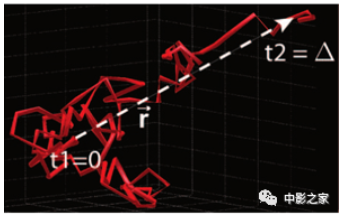
图1 示意图显示了单个水分子在扩散过程中由扩散驱动的随机位移轨迹(红线)。虚线(向量r)表示在T1=0到T2=∆的扩散时间间隔内的分子位移距离。
为了说明这一想法,我们可以进行一个假想的实验。让我们想象一下,我们在时间t=0时发射定量为N的水分子,并对其进行标记,我们分别测量它们在给定时间间隔Δ(以下称为扩散时间间隔)内的位移。我们假设每个位移距离为r,并计算被标记的所有水分子的位移距离的数量n。我们使用得到的数据绘制出单个方向上标记分子的相对数量(n/N)与位移距离(R)的直方图。大多数分子的运动距离较短,只有少数分子运动得更远(图2)。通常,自由水分子的位移分布呈一个高斯(钟形)函数。
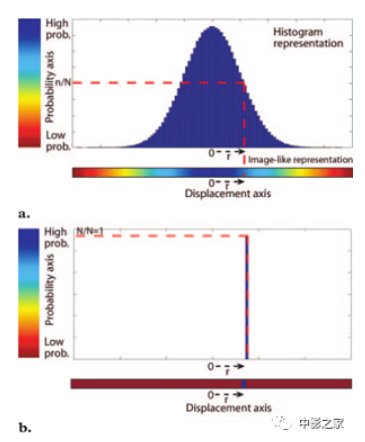
图2 (A)直方图显示了一维模型中由于扩散引起的典型位移分布。对于每个位移距离r(x轴),有一个相应的概率n/N(y轴),由此得到同一个体素中在规定时间间隔内被位移该距离的分子的比例∆(扩散实验的持续时间)。直方图的顶部以零为中心,表明大多数分子在t=0到t=∆时的位置相同。经过给定距离r的分子的比例由虚线红线表示。水平颜色条显示相同的高斯分布,其中蓝色表示高概率位移,红色表示低概率位移。(B)直方图表现出典型的通量引起的位移分布(即非零平均位移)。所有的分子都移动了给定的距离r,如n/N=1所示。
在37℃,扩散时间间隔为50毫秒时,特征距离(高斯分布的标准差)通常为17,大约32%的分子移动了这么远,而只有5%的分子移动了超过34微米。
如图2所示,直方图对于一维数据的显示是足够的,但要将其用于可视化多维位移中就需要对概率进行颜色编码。利用这样的方式,可以将一维位移轴转变为一个可视化彩色的位移轴(x轴),其中蓝色代码代表高概率,红色代码代表低概率(图2)。据此,我们可以用这样的三维轴来表示实际的三维(3D)扩散,对于通过三个相交平面上的位移概率用颜色编码(图3a)。图像的中心体素是原点,且它的概率值,或者分子(n/N)的比例在扩散时间间隔内不经历移位。一个简单实用的类比是将染料滴进一杯水里。在t=Δ拍摄的照片上,染料将被稀释(扩散),而相对颜色密度则表示染料分子在给定距离内被置换的比例。
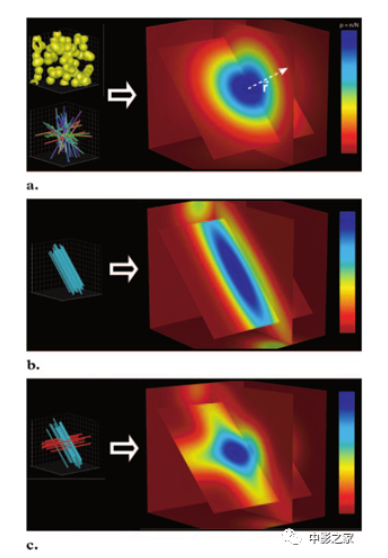
图3 单个体素内的扩散。(A)图显示了包含球状细胞(左上)或相交的随机定向管状结构(如轴突)的体素中的3D扩散概率密度函数。这种大致呈钟形的3D位移分布产生了对称的图像(中心),因为没有优先的扩散方向。这种分布类似于不受限制的扩散,但由于存在阻碍分子位移的势垒,所以分布更窄。图像的中心(r向量的原点)表示在扩散时间间隔内未被置换的分子的比例。颜色条(右侧)显示了颜色编码中用于表示概率的光谱,从红色表示的最低值到蓝色表示的最高值。(B)图显示了所有轴突在同一方向上排列的体素内的扩散概率密度函数。移位分布呈雪茄状,与轴突一致。(C)图表显示了包含以90°角相交的两组纤维的体素内的扩散概率密度函数。分子位移分布产生一个十字形。
均匀介质中的扩散可以很好地描述为高斯分布。根据分子的类型、介质的温度和允许扩散的时间不同,分布会更宽或更窄。
高斯分布类扩散由一个参数控制:方差(δ²)。方差反过来又取决于两个变量,因此δ²=2*D*Δ,其中D是扩散系数,表示介质的黏度或分子置换的难易程度。在37℃时,水分子的扩散系数约为D=3*10-9m²/sec。由于分子被置换的时间可能更长,扩散时间间隔越长,差异就越大。
分子位移、扩散和通量
我们使用术语位移分布来描述成像体素内水分子的群体行为。与位移分布等价的是位移概率密度函数和分子位移图像。在本文中,这些术语可互换使用。当分子单独被热能搅动时(即,当分子通过扩散过程发生置换时),位移分布居中。这意味着分子群体的平均或净位移为零。除热能以外的其他因素也可能对分子位移起作用。例如,管道中的压力梯度就可能会影响分子位移。在没有湍流和摩擦的理想环境中,所有分子都经历了相同的非零位移r。这样的设置产生了非常不同的位移分布,其中直方图在除了位置r之外的任何地方都为零,位置r的值为n/N=1(图2b),因为所有的分子都被移动了相同的距离。这种类型的位移称为磁通。在助熔剂中,分子在非零的平均距离上移动,扩散和通量通常同时发生,但在本文中我们只关注扩散。因此,位移一词将被更具体的术语扩散所取代。
复杂介质中的扩散
如前所述,一杯水中的分子是随机运动的,但它的运动轨迹不能超出杯子。同样的道理也适用于不透水的球体内的水分子,这些球体类似于水杯(图3a)。水分子在球体有限的空间内扩散,球体外的水分子在球体周围随机运动。因此,当组织内含有不透水球体与组织内无不透水球体时,相同体积内相关联的水分子位移分布大不相同。这一差异反映了水分子限制的存在。由于球体内部的分子不能移动到球体之外,而球体外的分子又不能穿透球体,预期的位移距离将会减小,由此产生的位移分布的形状就很难预测,但如果扩散时间足够长,它将或多或少是钟形的,并且明显比无限制扩散的分布窄(图3a)。与自由扩散一样,此时水分子的位移仍是各向同性的,没有择优方向。为了接近生物现实,我们可以向装水的玻璃杯中放入一组带膜的半透球,水分子可以在一定的阻力下穿过这些半透球。这将产生一个新的位移分布,它不像含不透水球的体积那样窄,但比自由扩散的体积窄。
生物组织是高度不均匀的介质,由不同扩散系数的隔间和屏障组成。细胞组织结构可以被看作是一组由网状隔室组成的多孔排列结构。在扩散驱动的随机置换过程中,水分子的运动受到隔室边界和其他分子障碍的阻碍,与无限制扩散时预期的扩散距离相比,实际扩散距离减小。神经细胞组织的一个决定性因素是它的纤维状结构。神经元组织由紧密排列的轴突组成,这些轴突被神经胶质细胞包围,呈束状结构。水分子的微观运动在垂直于轴突方向上受到的阻碍比平行于轴突方向的更大(图3b)。因此,分子平行于纤维方向的位移通常大于垂直于纤维方向的位移。这时的扩散性质随扩散方向变化,表现为普遍的各向异性,不再像无限制扩散那样表现为各向同性和呈高斯分布,而是呈雪茄形分布。如果组织含有不同走向的纤维,分布可能会更加复杂(图3c)。
实验证据表明,白质中的分子扩散呈各向异性的主要原因不是髓鞘,而是细胞膜(图4)。单个轴突的髓鞘化程度和细胞堆积密度仅对分子的各向异性具有调节作用。此外,轴突运输、微管和神经丝在磁共振成像测量的各向异性中似乎也只起到很小的作用。
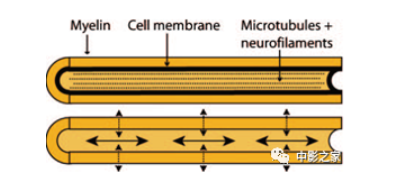
图4 示意图显示了导致扩散各向异性的细胞元素。
第二部分:扩散对比编码的基本原理
由六维图像表示的扩散
用计算机断层扫描(CT)或磁共振成像(MRI)获得的图像数据通常是3D数据。3D空间中的每个位置都与一个灰度级相关联,该灰度级编码了CT的线性衰减系数或MR成像的相对信号强度。在数学术语中,3D图像是位置变量p(3D向量)的函数,并且被指定为ƒ(p)。处在大脑不同分区位置的细胞结构差异很大。因此,如果在大脑不同位置(体素)测量局部位移分布情况,则会得到不同的位移分布结果。为了正确描述这种介质中的分子扩散,每个体素位置p须分配一个扩散概率密度函数(等价于位移分布)。由于扩散概率密度函数的视觉表示是3D图像,因此两个变量p和r的组合的自然结果是六维(6D)图像。
6D图像充分描述了非均匀介质中的扩散情况,因为它描绘了体素位置p中移动了距离r的分子ƒ(p,r)的比例(图5)。不同于CT或常规MR成像仅为每个单独的位置分配单个灰度级,而需将每个位置p与其编码后分子位移的新的3D图像相关联。得到的6D图像表示三个位置变量的函数(3D位置向量p)和三个位移变量(3D位移向量r)。这个多维的概念对于非数学专业的人来说可能不是直观的,但对于理解扩散成像原理却是必不可少的。

图5 左侧图像显示标准成像方法为每个3D位置p提供一个值(灰度级)。该值或灰度级可以编码为CT成像X射线衰减系数或MR成像相对信号强度。右侧图像显示,在扩散成像中,每个3D位置p(体素)与灰度级不相关,与编码该体素中分子位移分布的3D图像相关联。在坐标p,r处测量的值-ƒ(p,r)-表示体素中移动了给定距离r的分子的比例。
在三维空间中表示6D数据
在标准3D成像中,位置p的函数数据与其显示在监视器上以灰度级编码的功能强度区段之间几乎没有差别。两者之间的重要区别表现在当数据为六维数据时,因为六维数据不能直接表示,必须使用特定的计算机可视化技术将六维数据进行简化仅显示其主要特征。通常,在扩散成像中,相比于获得详细的扩散轮廓我们对确定最快速的扩散方向更感兴趣,因为与后者相对应的可能是轴突或其他纤维结构的方向。也可用等值面代替扩散概率密度函数,等值面即所有具有相同值的点的表面,其中ƒ(R)的值是常量(图6)。一种对噪声不太敏感但更常用的技术,其可根据位移分布计算出取向分布函数(图6、图7)。取向分布函数可以被认为是变形球体,其在给定方向上的半径与该方向上的扩散概率密度函数值之和成正比。为了便于可视化,我们根据扩散方向([x,y,z]=[r,b,g])对表面进行颜色编码,其中r=红的,b=蓝色的,还有g=绿色。由此可以为截面中的每个单独的MR成像体素绘制取向分布函数或等值面(图8)。
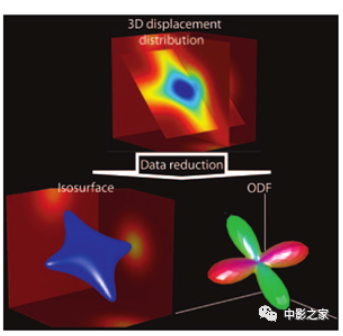
图6 显示了可用于简化3D扩散数据的可视化表示的两种方法:用等值面替换位移分布和计算取向分布函数(ODF)。
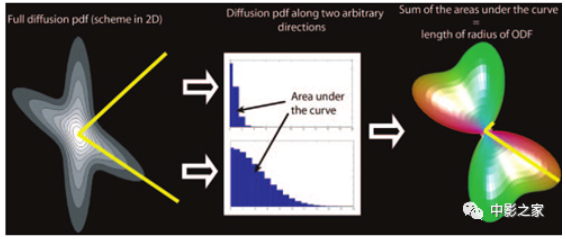
图7 显示了如何计算和表示取向分布函数(ODF)。左图:通过图案化的3D置换分布的截面图像。沿两个轴(黄线)计算取向分布函数的值。中心:直方图表示沿两个轴的位移分布。沿这些轴的方向分布函数的值等于每个轴的曲线下的面积。从这个例子中可以发现在一个方向上的扩散比在另一个方向上要小得多。右图:曲线下面积之和由变形球体表示,其中两个长度不同的半径(黄线)分别对应于小扩散和大扩散。为了计算方向分布函数,需要计算每个方向的曲线下面积。

图8 脑冠状切面的方位分布函数图。对于每个脑位置p,绘制一个方向分布函数来表征局部扩散概率密度函数。很容易辨认出皮质脊髓束,其中的主色是蓝色,以及穹隆体部,其中红色是主要的。更难看到的是扣带和弓形束,主要用绿色描绘,小脑梗中部,用红色描绘。
扩散对比度编码的一般描述
为了描述位移分布,扩散必须与磁共振成像时测量的信号强度相关联。如前所述,水分子在热能的作用下随机运动。1950年,Hahn注意到自旋(即水分子中的氢质子)质子在非均匀磁场中的运动导致了信号强度的降低。1956年,Torrey在MR光谱学实验中建立了用于描述自旋磁化强度的基本方程(6)。从那时起,这些方程就被认为是扩散成像中最基本的方程。
1965年,Stejskal和Tanner公布了第一个测量扩散的磁共振波谱实验的结果。在实验中,研究人员使用了脉冲梯度自旋回波(SE)序列,这是一种可以观察的技术,即沿磁场梯度方向运动的自旋质子根据其所在梯度轴的位置而暴露在不同的磁场强度中。众所周知,在磁共振成像中,外加磁场会影响自旋质子的相位,影响的程度取决于外加磁场的强度。与经典SE序列相比,脉冲梯度SE序列包括两个额外的扩散梯度脉冲(图9)。该序列中的两个梯度脉冲中的第一个引入相移,该相移取决于t=0时自旋质子所处位置梯度的强度。在施加第二梯度脉冲之前,施加180°RF脉冲来重聚由第一梯度脉冲引起的相移,第二梯度脉冲在t=Δ处再次引起相移。由于扩散编码梯度导致场强(即相移)随位置变化,所以在两个脉冲期间沿梯度轴保持在相同位置的所有自旋质子将返回到其初始状态。然而,在第二次脉冲期间,移动的自旋质子将受到不同的场强的影响,因此不会返回到它们的初始状态,而是会经历第二次相移,从而导致测量的MR信号的强度降低。位移距离越长,相移越大,信号衰减越大。因此,合成的图像在沿施加的扩散梯度的扩散较高的区域中显示为低信号。
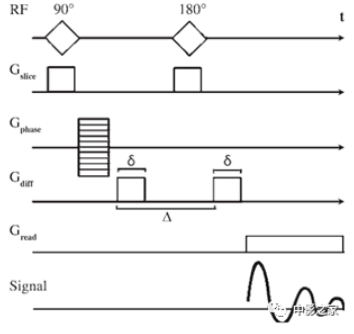
图9 示意图显示用于扩散磁共振成像的脉冲梯度SE序列。两个扩散编码梯度(Gdiff)脉冲被添加到标准SE MR成像序列中,以引入与分子沿梯度方向的位移成比例的相移。δ=扩散编码梯度的持续时间,∆=扩散时间间隔,Gphace=相位编码梯度,Gread=读数梯度,Gslice=节段选择梯度,RF?=射频脉冲,t=获取时间。扩散编码梯度通常用矢量q来表示,它等于γ*δ*Gdiff的乘积,γ是旋磁比;因此,它代表有效扩散梯度。
扩散梯度可以表示为3D向量q,其方向为扩散方向,其长度与梯度强度成正比。梯度强度,或者称为扩散加权,有时用b值来表示,b值与梯度强度q的平方和扩散时间间隔的乘积成正比(b~q²*Δ)。
与k-空间类似的q-空间
根据基本的磁共振成像原理,我们在采集序列的特定时刻,运用不同方向和不同强度的梯度,对测量的信号进行相位和频率编码。测量的信号值被有秩序地放在被称为k空间的坐标系中,按执行计划填充到k-空间。要将k空间的原始MR数据转换为位置编码的视觉图像,需要对其进行傅里叶数学运算(图10)。

图10 示意图显示了获得标准位置编码磁共振图像的过程。
首先,将通过相位和频率编码后的MR信号被填充到k空间(用于组织信号测量的坐标系)。接下来,对原始数据(k空间图像)进行傅里叶转换,以重建出标准空间位置中的图像。
磁共振扩散成像的过程与此类似。让我们首先定义一个新的3D空间,称为Q-空间,其坐标由向量q定义。应用单个脉冲梯度SE序列产生一个扩散加权图像,该图像对应于q空间中的某一位置,或者更准确地说,其对应于大脑每个特定位置q处的扩散加权信号强度。在强度和方向上重复变化的梯度(即,随着q的变化)序列在整个q空间中进行数据采样。与常规MR成像的数据类似,傅里叶变换被应用于k-空间,对应于大脑解剖位置的q-空间数据也须进行傅立叶变换。结果得到每个大脑位置中质子的位移分布(即体素)(图11)。换句话说,脉冲梯度SE序列的单次激发产生了具有给定扩散加权的一个脑图像。让不同的扩散加权多次重复是进行q空间数据采样所必需的;其结果就是数百幅大脑图像反映了所使用的特定扩散的加权值。我们想象将采集到的数据重新排列,以便在每个大脑位置有一个由数百个值组成的q空间信号样本,并让傅立叶变换将其原始的q空间数据与扩散概率密度函数相关联(图12)。
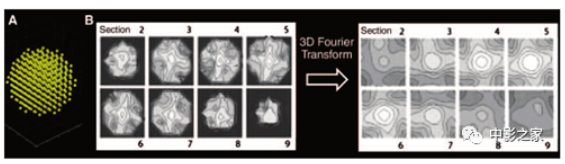
图11 显示了对于一个体素(一个大脑位置)获得3D扩散概率密度函数的过程。在代表Q空间的3D网格A中,每个黄点对应一个MR信号采样点。通过改变脉冲梯度SE序列的扩散梯度(Q矢量)的方向和强度,在每个点对信号进行采样。通过一次脉冲梯度SE序列的激发,同时对每个脑位置的Q空间中的一个点进行采样,结果得到一幅扩散加权图像。在B图左侧显示了在Q空间中针对特定大脑位置(一个体素)采样的MR信号的截面,而右侧显示了在Q空间中执行MR信号的3D傅里叶变换后在同一体素中的扩散概率密度函数。十字形扩散概率密度函数出现在脑干的体素中,皮质脊髓束的轴突与小脑脚中部的轴突相交。

图12 在脉冲梯度SE序列中,随着扩散梯度方向和强度的变化而获得的一系列磁共振扩散加权图像。每幅图像都显示了在Q空间中的一个采样点(一个黄点)的信号。Q空间中的每个采样点对应于扩散梯度的特定方向和强度。
q空间总是在特定的扩散时间间隔内被采样,该时间间隔由两个梯度脉冲之间的间隔时间决定。可以通过改变扩散时间间隔以获得不同的扩散结果。例如,间隔越长,方向分辨率越好。想象一下轴突内的扩散:当采用一个很短的扩散时间时,分子在每个方向上都有相同数量的扩散。随着扩散时间延长,当分子到达轴突壁时,垂直于轴突方向的扩散停止,而沿轴突长轴的扩散继续。因此,较长的扩散时间增加了不同方向上的信号之间的区别;然而,较长的扩散时间也会导致信噪比的降低。
为了描述采样q空间中应用的参数,通常使用术语“b值”。b值与扩散时间间隔和扩散梯度强度的平方成正比。应该将所有扩散图像与非扩散加权的参考图像(标准SE图像)即扩散梯度值为零(q=0.b=0)的图像进行比较。
扩散光谱成像
扩散光谱成像可以被理解为扩散成像的参考基础,因为它是先前推导的原理的实际措施,是以坚实的物理理论为基础的扩散成像技术。适用于活体成像,且它提供了足够稠密的q空间信号样本,通过使用傅立叶变换从该样本中推导出位移分布。该技术最先由Wedeen等人提出。
如果遵循既定的做法,连续获取515个扩散加权图像,每个图像对应不同的Q向量,这些图像被放置在具有五个晶格单元半径的球体内的立方晶格上。晶格单位对应于不同的b(或q)值,从b=0(对应于球体的中心点)到通常的b=12,000sec/mm²(这是一个非常高的b值)。傅立叶变换是在Q空间数据上计算的。如果成像矩阵的大小为128*128*30,则需要进行与计算每个脑位置的扩散概率密度函数相同次数的傅立叶变换运算。
传统上,515幅图像被认为是获得高质量数据所必需的,尽管获取该数量的图像非常耗时。随着近年来MR成像硬件和成像技术的改进,以及鉴于最近的其他经验,采样点数可以适当减少;通过仅对q空间中的半球进行采样,可以用大约257甚至129幅图像重建出概率密度函数。当然,信噪比和角分辨率可能会受到相应的影响。因此,双侧大脑半球的成像时间可以从45-60分钟减少到10-20分钟,这一时间使该技术在临床环境中变得可行。
通过在q空间上对每个大脑部位进行傅里叶变换,得到了该部位和位移的6D图像。每个部位的扩散由位移分布或概率密度函数来表示,它提供了对扩散的详细描述和对高度复杂的纤维组织(包括纤维交叉)的出色分辨率。由于扩散光谱成像主要用于只需要方向信息的纤维束成像,因此通过对每个方向上的扩散概率相加来将概率密度函数简化为取向分布函数(图7)。
来源:中影之家
相关链接
查看更多