作者：诸暨市中心医院 冯璐霏

本文分享自Radiographics上的一篇综述：

了解扩散磁共振成像技术:从标量扩散加权成像到扩散张量成像及其他。

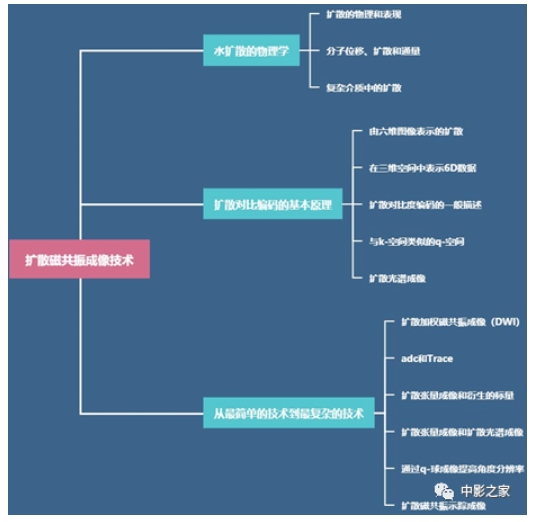
整篇文章思维导图如下:

第三部分:从最简单的技术到最复杂的技术。

扩散加权磁共振成像是扩散成像最简单的形式。扩散加权图像是重建扩散光谱成像中的完整概率密度函数所需的分量之一。扩散加权图像是在一个梯度方向上应用单个脉冲梯度SE序列的未处理结果，它对应于Q空间中的一点。尽管这样的图像相当简单，但它确实包含了一些关于扩散的信息。在图13中，胼胝体左侧压部呈亮色，右侧压部呈深色。在诸如右侧胼胝体压部之类的区域中，主扩散方向与应用的扩散梯度一致，该区域信号强度明显降低，因此图像上的区域看起来更暗。在脑室中，扩散在所有方向上都是自由的和充分的，包括施加的梯度方向，因此整个脑室看起来是暗的。尽管弥散加权成像很简单，但它经常用于中风的研究。事实上，在急性卒中中，局部细胞肿胀增加了对水流动性的限制，因此由于病变区域的高信号强度而出现明亮的影像表现。扩散加权成像的优点是采集时间短，因为只需要一幅图像。

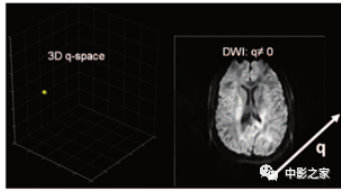
3DQ空间中单点信号采样的扩散加权图像(右)(左)。沿外加梯度方向扩散强烈的脑区(q)。因为去相导致测量信号的减少，所以看起来更暗。

扩散加权成像的问题是，对结果图像的解释并不直观。为了解决这个问题，让我们假设扩散是没有限制的，因此它的位移分布可以用一个自由扩散物理模型来描述，这是一个三维各向同性的高斯分布。在该模型中，物理扩散系数D被ADC替换，ADC是从公式ADC=-bln(DWI/b0)导出的，其中DWI是如上一节中定义的针对特定b值和扩散梯度方向的扩散加权图像强度，而b0是没有扩散加权的参考图像。因此，要获得ADC值的图像，需要进行两次采集。

ADC非常依赖于扩散编码的方向。为了克服这一限制，可以进行三次正交测量并对结果进行平均，以获得更好的扩散系数近似值。这种方法等同于从扩散张量导出Trace，下一节将更详细地描述。

对于ADC成像，我们假设扩散遵循自由扩散的物理模型，并用各向同性的高斯分布来描述。这个模型往往过于简单化，特别是当我们对轴突束的方向感兴趣时，其中的扩散被认为是各向异性的(即，在所有方向上并不相同)。为了讨论的目的，让我们假设扩散仍然是高斯的，但可能是各向异性的。换句话说，扩散可以是雪茄或圆盘形状，但也可以是球形的，如各向同性扩散。各向异性高斯分布有六个自由度，而不是一个。

因此，为了符合我们的模型，我们必须使用Q≠0(扩散加权图像)对Q空间中的至少6个点进行采样，并使用Q=0(参考图像)对一个点进行采样。通常，使用大约1000sec/mm²的b值。为了将生成的数据与模型相匹配，我们必须解决一组就像之前给出的六个方程式。 结果是扩散张量(而不是扩散系数)与高斯协方差矩阵(而不是高斯方差)成正比。这个扩散张量是一个3*3矩阵，它完全描述了三维空间中的扩散，假设位移分布是高斯的。扩散张量通常用椭球体或取向分布函数表示。

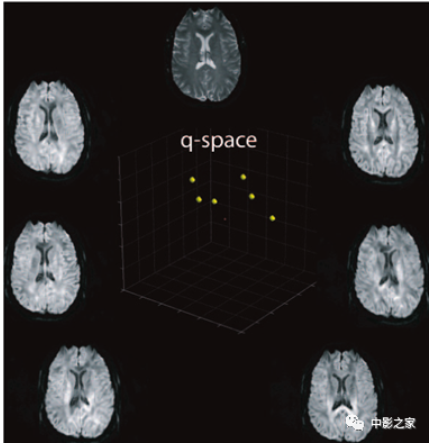
扩散张量成像获得的一系列扩散加权图像，其中Q空间在至少六个不同方向上被采样，其中获得非扩散加权参考图像。对于每个采样，扩散梯度的方向而不是强度都会改变。

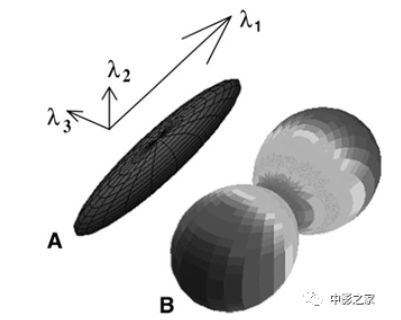
扩散张量图。在A中，扩散张量表示为椭球体(等值面)，其主轴沿特征向量(λ1，λ2，λ3)。在B中，扩散张量表示为取向分布函数。

扩散张量的数学性质使得从扩散张量图像中提取几个有用的标量度量成为可能。平均扩散，也称为迹线，通过对矩阵的对角元素求平均来计算。结果是如图16a所示的图像，并且与通过在三个正交方向上估计ADC而获得的结果相同。扩散极大值的方向称为扩散的主方向，可以通过计算张量的特征向量和特征值直接获得。特征向量彼此正交，并用特征值描述张量的性质。本征值按λ1 λ2 λ3排序，每个特征值对应一个特征向量。与最大特征值(λ1)对应的特征向量是扩散的主要方向。如果特征值彼此显著不同，则称扩散是各向异性的。如果λ1比第二本征值λ2大得多，则扩散是雪茄形的(图15)。如果λ1和λ2相似但比λ3大得多，则称扩散为平面或圆盘状。当所有特征值近似相等时，扩散是各向同性的，并且可以表示为球体。

特征值之间的关系反映了扩散的特点。为了用标量值描述扩散的形状，分数各向异性是最常用的。然而，其他措施，如Westin等人所描述的措施，也是可用的。分数各向异性是通过将每个本征值与所有本征值的平均值(〈λ〉)进行比较来计算的，如下式所示：

其中，Fa是分数各向异性。一段扩散张量的分数各向异性如图16b所示。

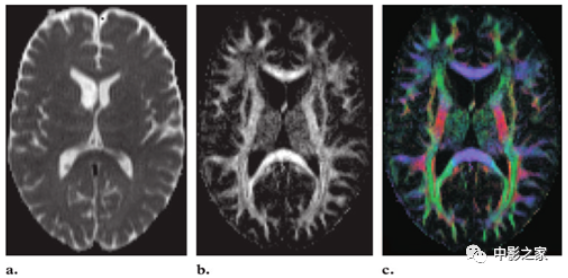
从扩散张量成像中提取标量值。(A)图像显示平均扩散，这是扩散张量的踪迹。在三个垂直方向上平均的ADC图像将具有相似的外观。(B)图像显示了分数各向异性，该分数各向异性是根据扩散张量的特征值计算得出的。(C)彩色编码图像显示了扩散的主要方向，红色、蓝色和绿色分别表示沿x、y和z轴的扩散。颜色强度与分数各向异性成正比。

椭球体或取向分布函数是使扩散张量数据可视化的最准确的方法，但有时很难在显示监视器上的成像部分上表示它。根据扩散的主要方向对扩散数据进行颜色编码可能是可视化数据的更实用的方式。在我们使用的颜色编码系统中，红色对应于沿上下轴(x轴)的扩散；蓝色对应于沿横轴(y轴)的扩散；绿色对应于沿前后轴(z轴)的扩散。

颜色的强度与分数各向异性成正比。该颜色编码方案的一个例子如上图所示。

扩散张量模型在只有一个纤维群(即纤维沿一个轴排列)的区域表现良好，它很好地描述了纤维的取向。

然而，由于它不能用于同时映射多个扩散极大值，因此在多个纤维种群沿相交轴线对齐的区域中该算法失败。在这些区域，需要能够提供更高角度分辨率的成像技术。

由于应用扩散梯度和自由度的数量有限，扩散张量模型不能解决纤维交叉问题。相比之下，扩散波谱成像并不是建立在任何关于扩散的特定假设上。因此，其解析扩散概率密度函数的能力仅取决于Q空间的分辨率，而其解析光纤交叉的能力仅取决于相关的角分辨率。在图17中，使用这两种方法获得的图像并列在一起。差异最显著的区域是桥脑在皮质脊髓束和小脑中脚交叉的地方，以及半卵圆中心在皮质脊髓束穿过胼胝体和弓状束的地方。

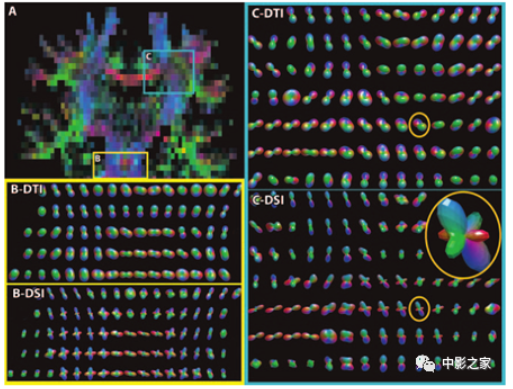
包含纤维交叉区域的扩散张量成像和扩散波谱成像的比较。在A中，彩色编码的冠状扩散图像显示了桥(B)和半卵圆中心(C)，其中扩散由扩散张量图像(B-DTI，C-DTI)和扩散波谱图像(B-DSI，C-DSI)来描述。在脑桥，小脑中脚横跨皮质脊髓束。在半卵圆中心，皮质脊髓束横跨胼胝体和弓形束。在圆形截面(C-DTI、C-DSI)中可以看到，扩散张量成像不能分辨纤维交叉，而扩散波谱成像能够分辨纤维交叉。

在采集时间方面，扩散张量成像比扩散波谱成像具有明显的优势，因为它只需要最少七张图像，而扩散波谱成像需要数百张图像。扩散光谱成像以前需要很长的采集时间，但随着不断的改进，采集时间正在减少。

我们已经看到，一方面，扩散张量成像在许多大脑区域不足以准确地绘制主干的方向。

另一方面，我们希望有一种比扩散光谱成像更快的技术，这对于常规的临床应用来说是耗时的，尽管这方面的改进目前正在评估中。q-球成像是一种尝试将这两种技术的最佳属性结合起来。尽管出于说明的目的，我们决定只讨论q-球成像，但是还有许多其他的启发式方法，例如基于持久角结构的方法和球面反卷积方法。所有这些技术都基于相同或几乎相同的方案，该方案包括对q空间中具有恒定高b值的球体内的信号进行相当密集的采样。通过使用各种算法从所得到的数据估计取向分布函数。

与扩散张量成像一样，q-球成像基于扩散概率密度函数形状的假设。这一假设很复杂，需要比本文提供的更深入地考虑信号在q空间中的空间频率成分。在这里，我们只考虑一种特定类型的扩散概率密度函数，q-球成像为其提供了足够的基础。我们假设体素内部的隔间由一组具有不透水墙的非常薄的直管组成。假设管道内的水分子沿管道长度均匀扩散，但没有横向运动。在这种情况下，扩散概率密度函数看起来像一个枕头。使用该模型，可以通过在具有固定半径的球体上的q空间中的采样点来重建扩散，并且具有较高的b值(通常为＞4000 sec/mm²)。通过使用Funk-Radon变换重建数据，该算法可以描述如下：假设我们想知道与北极对应的方向上的扩散强度(即，方向分布函数的值)，并且已经在全球范围内对MR信号进行了采样。如果我们将沿赤道测量的信号强度的值加在一起，总和将与北极的扩散强度成正比。例如，如果我们将北极的位置重新定义为洛桑，并相应地重新定义赤道，则可以用类似的方式计算洛桑的方位分布函数值。同样的方法也可以用于重建地球上任何点(例如波士顿、斯德哥尔摩、布鲁塞尔)的方位分布函数。

显示在q球成像中，具有恒定b值的壳上的点是在q空间中获得的。重建逼真的方位分布函数至少需要60幅图像。

与扩散张量成像不同，q-球成像可以解释单个体素内的多个交叉纤维，因此可以提供对复杂纤维结构区域的逼真描述，如半卵圆中心和脑桥。

q-球成像获得的图像与扩散光谱成像获得的图像相似。然而，必须进行进一步的验证研究，以确定q-球成像是否提供了对大脑所有区域的高质量描述，以及重建的图像是否准确。

脑纤维束成像是一种渲染方法，用于改善来自大脑扩散成像的数据的描述。虽然详细讨论跟踪技术超出了本文的范围，但有必要简要介绍一下，因为示踪技术是为帮助图像解释而开发的最强大的工具之一。纤维束成像的主要目的是通过整合最大扩散相干性的路径来阐明组织的定向结构。纤维在大脑中的生长是通过体素到体素扩散最大值的方向的方式进行的。纤维束造影术所描绘的纤维通常被认为代表单个轴突或神经纤维，但从物理角度看，它们更准确地被视为遵循局部扩散峰值的快速扩散线，并且仅大体反映轴突的结构。这一区别是有用的，因为对于给定的成像分辨率和信噪比，最大扩散相干线(即计算机生成的纤维)可能与某些大脑中的轴突结构不同。纤维束造影术为人类神经元解剖的磁共振成像提供了更多的信息和兴趣。

根据用于获得扩散数据的扩散成像方式的不同，用光迹照相术获得的连通性图也不同。例如，扩散张量成像提供了实际位移分布的高斯近似，由于该分布的表示仅限于椭球体的变化，因此该方法在跟踪成像结果中产生了各种偏差。相比之下，扩散光谱成像和光道成像克服了许多这些偏差，并允许更真实地绘制连接性地图。跟踪成像的结果还取决于所使用的跟踪算法。来自扩散张量成像的确定性纤维跟踪使用扩散的主要方向来积分图像上的轨迹，但是忽略了在扩散张量成像数据中纤维取向通常是不确定的这一事实。为了克服数据的这一局限性，Hagmann和他的同事以及其他研究人员研究了基于张量作为纤维取向概率分布的统计纤维跟踪方法。

将纤维束成像应用于数据，例如通过扩散光谱成像或q-球成像获得的数据，结果是描绘了具有更复杂的几何学。与使用扩散张量磁共振成像数据的纤维束成像相比，这种方法获得了更大的复杂性，这是因为考虑了许多可以分辨或区分的纤维之间的交叉点。

来源：中影之家